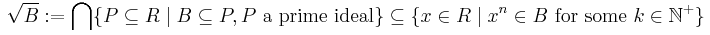Semiprime ring

In ring theory, semiprime ideals and semiprime rings are generalizations of prime ideals and prime rings. The class of semiprime rings includes semiprimitive rings, prime rings and reduced rings.

In commutative algebra, semiprime ideals are also called radical ideals.

Most definitions and assertions in this article appear in (Lam 1999) and (Lam 2001).

1 Definitions
2 General properties of semiprime ideals
3 Semiprime Goldie rings
4 References
5 External links

Definitions

For a commutative ring R, an ideal A is a semiprime ideal if A satsifies either of the following equivalent conditions:

If x^k is in A for some positive integer k and element x of R, then x is in A.
If y is in R but not in A, all positive integer powers of y are not in A.

As with prime ideals, this is extended to noncommutative rings "ideal-wise". The following conditions are equivalent definitions for a semiprime ideal A in a ring R:

If J^k⊆A for a positive natural number k and ideal J of R, then J⊆A.
If J^k⊆A for a positive natural number k and right ideal J of R, then J⊆A.
If J^k⊆A for a positive natural number k and left ideal J of R, then J⊆A.
If xRx⊆A for some x in R, then x is in A.

The ring R is called a semiprime ring if the zero ideal is a semiprime ideal. In the commutative case, this is equivalent to R being a reduced ring, since R has no nonzero nilpotent elements. In the noncommutative case, the ring merely has no nonzero nilpotent right ideals. So while a reduced ring is always semiprime, the converse is not true^[1].

General properties of semiprime ideals

To begin with, it is clear that prime ideals are semiprime, and that for commutative rings, a semiprime primary ideal is prime.

While the intersection of prime ideals is not usually prime, it is a semiprime ideal. Shortly it will be shown that the converse is also true, that every semiprime ideal is the intersection of a family of prime ideals.

For any ideal B in a ring R, we can form the following sets:

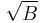$\sqrt{B}:=\bigcap\{ P\subseteq R \mid B \subseteq P, P \mbox{ a prime ideal} \}\subseteq\{x\in R\mid x^n\in B \mbox{ for some }k\in\mathbb{N}^%2B \} \,$

The set $\sqrt{B}$ is the definition of the radical of B and is clearly a semiprime ideal containing B, and in fact is the smallest semiprime ideal containing B. The inclusion above is sometimes proper in the general case, but for commutative rings it becomes an equality.

With this definition, an ideal A is semiprime if and only if 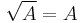$\sqrt{A}=A$ . At this point, it is also apparent that every semiprime ideal is in fact the intersection of a family of prime ideals. Moreover, this shows that the intersection of any two semiprime ideals is again semiprime.

By definition R is semiprime if and only if 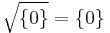$\sqrt{\{0\}}=\{0\}$ , that is, the intersection of all prime ideals is zero. This ideal 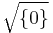$\sqrt{\{0\}}$ is also denoted by 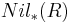$Nil_*(R)\,$ and also called Baer's lower nilradical or the Baer-Mccoy radical or the prime radical of R.

Semiprime Goldie rings

References

^ The full ring of two-by-two matrices over a field is semiprime with nonzero nilpotent elements.

Lam, Tsit-Yuen (1999), Lectures on modules and rings, Graduate Texts in Mathematics No. 189, Berlin, New York: Springer-Verlag, ISBN 978-0-387-98428-5, MR 1653294

Lam, T. Y. (2001), A first course in noncommutative rings, Graduate Texts in Mathematics, 131 (2 ed.), New York: Springer-Verlag, pp. xx+385, ISBN 0-387-95183-0, MR 1838439

External links

PlanetMath article on semiprime ideals